О возможности нового подхода к архитектуре наномира

КАРТА САЙТА

О возможности нового подхода к архитектуре наномира

Е.А. Андреев, Институт физики НАН Украины, Киев

evgalexandr@mail.ru

Предложен новый метод восстановления и прогнозирования геометрических взаимоотношений между атомами в произвольных атомных ансамблях. Основная идея метода основывается на гипотезе, что рассчитанные квантово-химическими методами поверхности нулевого градиента электронной плотности наиболее адекватно описывают «форму атома» в конденсированном веществе и с достаточной точностью могут быть аппроксимированы выпуклыми многогранниками определенной топологии.

Непрерывное заполнение пространства феноменологически найденным набором примитивных полиэдров типа Вороного-Дирихле (атомных доменов) позволяет правильно восстанавливать трехмерную структуру произвольных молекул, наноструктур, решеток металлов.

Заполнение приповерхностных областей полиэдрами из этого же базового набора дает возможность предсказывать характер взаимодействия произвольных атомных ансамблей между собой.

Ключевые слова: атомный домен, непрерывность, структура кристаллов, метод Вороного-Дирихле.

PACS numbers: 61.46.+w, 61.48.-c, 61.50.Ah , 61.50.Ks   63.20.dk, 68.47.-b

Введение

Для изучения структуры некристаллических систем часто применяются разнообразные геометрические методы, в частности подходы типа полиэдрального моделирования Вороного-Дирихле (ВД) [1]. К сожалению, они не применимы для малоразмерных наносистем и тем более одиночных молекул. Напомним, что полиэдром ВД (или атомным доменом) произвольного атома называется выпуклый многогранник, ограниченный плоскостями, которые проведены перпендикулярно через середины отрезков, связывающих соседние атомы. По этой причине построить полиэдр ВД для поверхностных атомов невозможно. В апериодических структурах часто имеются пустоты, которые также нарушают алгоритм построения полиэдров. В слоистых же структурах (например, графит) типы и параметры полиэдров на границах слоев значительно отличаются от усредненных значений.

Геометрические закономерности расположения атомов в клатратных соединениях (особенно в областях пустот) отмечают очень многие исследователи [2]. В частности, пустоты нередко имеют форму низкоразмерных фуллеренов типа С20, С24, С28 и т. д. Все это наводит на мысль, что как полиэдральное расположение атомов, так и топология самих полиэдров [3] далеко не случайны.

Поэтому идея нахождения общего подхода к описанию пространственного размещения атомов в конденсированном веществе на основе простых геометрических фигур (геометрических примитивов) представляется весьма продуктивной и методологически ценной по следующим соображениям.

Хорошо известно, что межатомная электронная плотность (ЭП) и ее градиент ∇ρ(x,y,z) - фундаментальные характеристики, которые поддаются расчету и экспериментально измеряются. Совокупность точек с ∇ρ(x,y,z) = 0 задает трехмерную поверхность нулевого потока, и с ее помощью также можно характеризовать размер и форму атома в веществе.

Современные прецизионные рентгеноструктурные данные и результаты хорошо апробированных квантово-химических расчетов [4] распределения ЭП между атомами показывают:

а) области пространства, ближайшие к отдельному атому (они также называются атомными доменами или бассейнами), сильно отличаются от сферы и напоминают выпуклые многогранники разной формы;

б) в пространстве между атомами существуют особые «критические точки», где электронная плотность имеет экстремальные значения. Эти точки совпадают либо с местом контакта 4-х атомных доменов, либо лежат на поверхности раздела атомных бассейнов.

Понятно, что квантово-механические объекты нельзя характеризовать такими чисто геометрическими понятиями, как линия или плоскость. Тем не менее АД как модельный объект может оказаться весьма полезным при геометрическом обосновании начальных условий квантово-химических расчетов.

Базовая идея

В настоящей работе рассматривается возможность отождествить геометрию поверхностей нулевого градиента ЭП (поверхностей атомных бассейнов) с топологией АД типа Вороного-Делоне и попробовать заполнить пространство атомной решетки таким образом, чтобы:
а) каждый атом находился в центре АД;
б) АД соединялись между собой непрерывным образом;
в) число контактирующих АД было не более 4;
г) пустоты в структуре и приповерхностное пространство также заполнялись АД;
д) число типов АД ограничивалось пространственными комбинациями соединенных равновеликих граней с числом сторон 4, 5 и 6.

Поиск закономерностей взаимного расположения атомов в веществе сводится к задаче выбора типа полиэдра и ориентации его для каждого атома таким образом, чтобы контактирующие полиэдры соприкасались между собой конгруэнтными гранями. Упрощение, которое используется в модели, заключается в замене трудно рассчитываемой поверхности нулевого градиента электронной плотности простым пересечением плоскостей.

От подходов типа Вороного-Дирихле модель отличается тем, что учитывает неэквивалентность взаимодействующих атомов – плоскость АД проходит в общем случае не через середину линии, соединяющей центры соседних атомов.

Поэтому для решения задач, когда известно взаимное расположение атомов и геометрия межатомного пространства, предложена модификация метода Вороного-Дирихле. Суть ее в том, что используется набор полиэдров ВД с 4, 5 и 6-угольными гранями 21 типа (рис.1).

Почему именно 21? Строго говоря, этот вопрос еще ждет ответа. В литературе известны математические обоснования существования максимального количества многогранников того или иного типа [5]. К сожалению, их результаты не удалось применить для нашего набора начальных условий. Поэтому использовался метод комбинаторного перебора с учетом ограничений на типы граней, равенство длин ребер и максимальный объем многогранника.

Первое, на что обращаем внимание – это выбор длины ребра АД (или длины стороны плоской грани). Наиболее естественным на атомном масштабе принять, что длина ребра равна одной атомной единице или Боровскому радиусу (R_B= 0.5296 À). Как показал анализ экспериментальных данных, этот параметр фактически задается абсолютными размерами домена атома водорода и межатомным расстоянием в молекуле H₂.

Второе – из всего множества возможных решений «неправильных» многогранников выбираем только такие, у которых степень напряженности (сумма среднеквадратичных отклонений длин ребер от эталона) меньше заданного предела.

И третье – для неправильных многогранников производим нормировку размеров таким образом, чтобы сумма длин всех ребер (периметр) равнялась эталонной длине, умноженной на число ребер.

Из числа известных правильных многранников выбраны всего четыре. Это куб, шестигранная призма, усеченный тетраэдр и додекаэдрон. Условие непрерывности заполнения пространства, а это одно из условий Плато для устойчивой пены [5], накладывает ограничения на использование этих регулярных многогранников в общей архитектуре ячеистого пространства.

Действительно, заполнение пространства кубами или гексагональными призмами – это самое простое решение с точки зрения геометрии. Однако в этом случае нарушается условие Плато о том, что в каждом узле должно сходиться 4 и только 4 ребра. Поэтому эти домены могут использоваться только как промежуточные в комбинации с другими типами доменов.

Выбор топологии базовых доменов

Додекаэдрон – наиболее подходящая фигура (из регулярных многогранников) для заполнения пространства. Однако при моноэлементном заполнении додекаэдронами некоторая часть объема остается незаполненной. Поэтому он также должен использоваться в комбинации с другими типами.

Усеченный тетраэдр – единственный домен с треугольной гранью. Вопрос об использовании треугольных граней открыт, поскольку общая теория пены говорит о неустойчивости такой структуры. Однако минералогия и молекулярная биология дают нам немало примеров существования таких форм.

Поскольку модель предполагается использовать для описания реальных атомных ансамблей, геометрия базовых доменов для нее выбиралась в соответствии с известной геометрией низкоразмерных фуллеренов с числом атомов углерода 24, 26, 28, 30, 32, 36, 40. Ограничения на максимальный объем домена определялись радиусом вписанной в него сферы, который в свою очередь задавался максимальным ковалентным радиусом атома Cs.

Поскольку все типы перечисленных многогранников не являются правильными, конкретные значения длин ребер (координаты узлов) задавались тремя условиями.

1. Средняя длина ребра в домене (длина периметра, деленная на число ребер) в точности равна боровскому радиусу R_B (1 а.е. = R_B = 0.529 Ǻ);

2. Среднеквадратичное отклонение длин ребер от R_B минимально;

3. Узлы каждой грани лежат в одной плоскости.

Выполнение всех вышеперечисленных условий и соображений дало набор из 21 «идеальных» АД, которые в принципе пригодны для непрерывного заполнения пространства в атомных ансамблях. Сразу следует указать, что понятие «идеальный» АД коррелирует с понятием «изолированный одиночный атом» и используется как «мягкая» заготовка при дискретизации пространства в реальных системах.

Рис. 1. Набор доменов, потенциально пригодных для восстановления трехмерной архитектуры ячеистого пространства произвольной наносистемы в модели «Атомные соты».

На рис. 1 показан внешний вид перечисленных элементов, классифицированных по количеству и типу граней, в них содержащихся. Принцип наименования таков: сначала указан тип грани (по количеству сторон) – q=4, p=5, h=6, затем количество граней этого типа в домене. Например – q2p8h12 означает домен, у которого две квадратные грани, восемь пентагональных и двенадцать гексагональных граней. Для двух типов p12h8 и p12h10 возможны по две геометрически разные конфигурации (геометрическая изомерия). Для их идентификации использованы кавычки (“).

Взаимоотношение атомов и атомных доменов

Для того чтобы установить работоспособность предлагаемого подхода, необходимо в рамках постулированных правил и принципов проверить модель на простейших атомных системах. Перечислим их еще раз:

– сочленять домены друг с другом будем конгруэнтными гранями;

– каждый из 92 атомов химических элементов поместим точно в центр соответствующего домена.

– поскольку грани имеют свои оси симметрии (4, 5, 6), осевая ориентация для простейших двухатомных систем не определена. Важно, чтобы узлы и ребра граней совпадали. Это и есть реализация принципа непрерывного заполнения.

Рассмотрим простейшую двухатомную систему – молекулярный водород. Ковалентный радиус известен, расстояние между ядрами – 0.741 Ǻ. Поскольку атомы тождественны, логично предположить, что занимаемые ими домены также одинаковы. Чтобы выяснить, какой домен и в какой ориентации при контакте друг с другом обеспечивает нужное расстояние, для каждого домена из базового набора вычисляются расстояния от центра домена до центров его граней. Компьютерный анализ возможных конфигураций выдал единственное решение – при сочленении двух доменов типа p12h2 гексагональными гранями расстояние между центрами доменов оказывается равным 0.741 Ǻ с точностью ~ 0.1%. Такое совпадение дает основание считать, что в случае молекулярного водорода атомы находятся в домене p12h2.

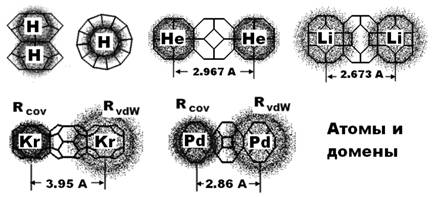
Укажем, что предыдущее и все последующие изображения, а также компьютерные расчеты выполнены в среде Maple-15. На рис. 2а показаны домены p12h2 с вложенными внутрь атомами водорода, с символично отображенным распределением электронной плотности в виде роя точек.

Анализ следующего двухатомного комплекса He₂ (R_cov = 0.32 Ǻ, R_vdW = 1.4 Ǻ, Dist_He-He = 2.967 Ǻ)   показывает отсутствие решения в множестве контактирующих пар одинаковых АД. И только введение промежуточного третьего домена успешно согласует геометрические атомные и доменные параметры (рис. 2 b).

Рис. 2. Примеры вложений атомов димерных комплексов в домены, обеспечивающие необходимое расстояние между центрами. Атомы схематично изображены роем точек, внешний размер которого равен ковалентному или Ван-дер-Ваальсовому радиусу: а – изображение молекулы H₂ в доменах p12h2 (вид сбоку и сверху); b – димер из атомов гелия в крайних доменах типа q6h8; c – димер Li-Li в доменах q6h12.

Разница между модельными и экспериментальными дистанциями, как и в случае молекулярного водорода, не превысила 0.1 % . Такое совпадение при столь простых начальных предположениях естественно вызывает законные вопросы. Насколько универсальна процедура, напоминающая детский конструктор? Чтобы ответить на этот вопрос, мы обратились к экспериментальным данным по расстояниям между атомами в димерах типа А-А [5..7]. Рассмотрим димер Li-Li.

Процедура компьютерного поиска выдает структуру из трех доменов типа q6h12, контактирующих между собой экваториальными гексагональными гранями. Атомы лития расположены в центрах крайних доменов, центральный же пустой. Опять же – расстояние между центрами атомов совпадает с табличными значениями с точностью до 0.001 ангстрема. Внешний вид комплекса показан на рис. 2 с.

Двухатомные комплексы

Справедливо ли столь идеальное совпадение и для более тяжелых атомов? Не всегда. На рисунках d, e показано геометрическое взаиморасположение димеров криптона и палладия. Как и в случаях легких атомов, димер Pd идеально вписывается в конструкцию из доменов типа q6h12, однако домены контактируют уже четырехугольными гранями. Правда, чтобы обеспечить совпадение предсказаний модели с экспериментальными данными, домен p12h8 нужно было «растянуть» на 5.2 %. Когда мы проверили работоспособность модели для известных двухатомных комплексов, оказалось, что примерно в половине случаев необходимо домены слегка деформировать путем сжатия или растяжения. Как правило, величина деформации находится в пределах ± 1–3 %. Кстати, для димера криптона она имеет максимальное значение.

Поскольку число разных атомов превышает число базовых доменов, в домене одного типа могут находиться разные атомы. «Предпочтение домена» конкретного атома задается несколькими факторами:

– условием непрерывности заполнения пространства;

– структурой электронных орбиталей (внутренней симметрией волновой функции атома);

– размером атома;

– типом (симметрией) домена.

И, наконец, наверно главное – типом симмметрии внешней электронной оболочки, которая для ряда атомов может меняться в зависимости от внешнего окружения..

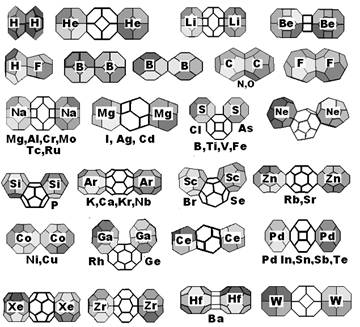
Рис. 3. Доменная архитектура двухатомных комплексов, построенная по данным межатомных расстояний, взятых из работ [8-11].

Доменная архитектура более чем 50 димеров показана на рис. 3. Как видим, одинаковые атомы расположены в разных АД и наоборот, разные атомы – в однотипных доменах. Например, Na, Mg, Al, Cr, Mo, Tc и Ru «предпочитают» домен q6h12. Атомы бора, титана, ванадия и железа в бинарных системах находятся внутри доменов q6h8.

Таким образом, модель заполнения «пустого» межатомного пространства доменами с образованием непрерывной структуры дает количественное объяснение межатомных расстояний в димерных комплексах.

После апробации на двухатомных системах подход был применен для полиэдрального описания массива одиночных молекул, некоторых кристаллов, малоразмерных наносистем. Поскольку структура простых органических и неорганических молекул восстанавливалась достаточно просто, было интересно применить полиэдральную модель для построения трехмерной структуры сильно напряженных молекул.

Молекулы и решетки

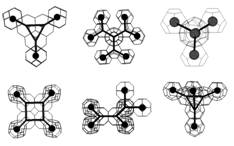
В работе [3] большое количество типов органических молекул сведено к 26 типам молекулярных графов. Как правило, это молекулы с необычной структурой типа тетраэдранов, кубанов и пропелланов, для которых модель молекулярных графов более адекватна по сравнению с другими. Оказалось, что молекулярные графы также воспроизводятся с точным соблюдением межатомных углов и расстояний (см. рис. 4 ), что подчеркивает универсальность модели. Интересно, что степень напряжения молекул, описываемых данными графами, коррелирует с величиной деформации полиэдров, включенных в эту трехмерную структуру.

Рис. 4. Примеры воспроизведения полиэдральной моделью 5 из 26 типов молекулярных графов Бейдера [4].

Возможность непрерывного заполнения пространства кристаллических решеток металлов демонстрируется на примере двух фаз Au (гексагональная и кубическая). На рис. 5 показаны поверхностные слои обеих фаз золота. Обращаем внимание, что различные фазы отличаются типом доменов, формирующих топологию пространства внутри металла, а ковалентный радиус золота лучше вписывается в домен q6h8, характерный для гексагональной решетки бета-фазы. Для полного совпадения параметров модельной и экспериментальной решеток домены деформированы в пределах нескольких процентов по-разному вдоль осей OZ и OX.

Рис. 5. Воспроизведение полиэдральной структуры решетки металлического золота. Слева – домены типа q6h12, характерные для α-фазы. Справа – домены типа q6h8, характерные для гексагональной β-фазы.

Столь простое и наглядное изображение структуры кристаллической поверхности позволяет сразу предсказать характер взаимодействия произвольного атома с поверхностью. Понятно, что если атом может находиться в доменах с наличием 4-х и 6-угольных граней, он будет в топологическом согласии (concordance) с поверхностью Au и взаимодействие может быть достаточно сильным. Кроме того, топология полиэдров однозначно указывает на места возможного связывания, что должно облегчить и ускорить общепринятые квантово-химические расчеты.

Слоистые структуры

В случаях, когда интересующий нас атом (или поверхность многоатомного ансамбля) топологически не совпадает с поверхностью кристаллической решетки, мы должны из имеющегося базового набора подобрать такую комбинацию полиэдров и такое их взаимное расположение, чтобы обеспечить согласованность граненых поверхностей обоих объектов.

Этот случай демонстрируется на примере реконструкции геометрии структуры графита при взаимодействии графеновых слоев между собой. Последовательность действий при решении этой задачи такова.

Шаг 1. Заполняем доменами классическую гексагональную структуру углеродного слоя (рис. 6 а). Решение простое и абсолютно однозначное – это совокупность АД типа p12h3, соединенных между собой гексагональными гранями. В этом случае и углы и дистанции между атомами без какой либо подгонки соответствуют табличным значениям. Но топология поверхности такова, что сочленить слои друг с другом невозможно. Поэтому (шаг 2) сверху и снизу от углеродных атомов заполняем пространство одинаковыми промежуточными слоями пустых АД двух типов (рис. 6 б, д). Затем (шаг 3) формируем промежуточный (согласующий) слой также из пустых АД (рис. 6 в). И уже он точно спрягает приповерхностные слои (рис. 6 г). В результате мы имеем трехмерную архитектуру из АД на (рис. 6 д). которая описывает реальную решетку графита (рис. 6 е) с межплоскостными расстояниями и их сдвигом относительно друг друга.

Рис.6. Последовательное заполнение межслойного пространства полиэдрами при воспроизведении решетки графита «из первопринципов»: а) – гексагональная решетка атомов углерода, упакованная в полиэдры типа з12р3; б) , г) – прилежащие (верхний и нижний) непосредственно к атомам углерода слои пустых доменов двух типов. Все грани контактирующих слоев конгруэнтно сопряжены друг с другом без зазоров; в) – промежуточный (сопрягающий) слой пустых доменов обеспечивает непрерывность заполнения пространства без нарушения топологии контактирующих доменов.

д) – верхний слой атомов углерода, сдвинутый относительно нижнего точно на табличные значения; е) – вид двух графитовых слоев сбоку. Пространство между слоями непрерывно заполнено пустыми доменами.

Приведенные выше примеры использования полиэдральной модели в столь разных разделах структурной химии и кристаллографии позволяют надеяться, что она применима для описания трехмерной архитектуры произвольных наносистем. Естественно, что полный ответ на границы использования модели может дать только практика. Пока же небольшой накопленный опыт позволяет начать работу по выяснению типов полиэдров, которые могут занимать известные химические элементы.

Обсуждение

1. Попытка упростить анализ трехмерной структуры различных атомных ансамблей с помощью понятия атомных доменов или атомных бассейнов, где аттрактором является атомное ядро, дала несколько неожиданные результаты. Не столь часто используемая характеристика распределения межатомной ЭП, такая как градиент и его векторное поле, оказалась весьма успешной для модельного представления «формы атома» в конденсированном состоянии.

Рассчитанная квантово-химическими методами поверхность нулевого градиента ЭП естественным образом ограничивает область влияния атома в системе и формирует ее некоторый пространственный образ. С другой стороны, методы полиэдрального моделирования (Вороного-Делоне и др.) также оперируют с похожими геометрическими формами. Использование двух, казалось бы противоположных представлений, приводит к одинаковым результатам вычисления межатомных дистанций.

2. Набор абстрактных геометрических примитивов, сконструированных по достаточно простым алгоритмам, приобрел физический смысл при введении в его основной геометрический параметр такой фундаментальной величины, как атомная единица длины или так называемый классический радиус электронной орбиты в атоме водорода. Конечно, пока рано говорить о какой-либо взаимосвязи физики и геометрии, тем не менее пища для размышлений существует.

3. Небольшое количество базовых полиэдров, способных объяснить геометрические характеристики разнообразных двухатомных комплексов, говорит о том, что набор внутренних симметрий атомов также достаточно ограничен. По крайней мере, это относится к бинарным атом-атомным взаимодействиям. Отсюда следует практически важный вопрос – насколько необходим учет многоэлектронных волновых функций в стандартных квантово-механических расчетах?

Выводы

Предложена и апробирована идея аппроксимации реальных поверхностей нулевого градиента электронной плотности одиночных атомов в конденсированном веществе деформируемыми полиэдрами Вороного-Делоне.

При выборе абсолютной длины ребер всех полиэдров равной 1 а.е. (Боровскому радиусу) комбинаторика сочленений многогранников конгруэнтными гранями обеспечивает

а) – непрерывное заполнение простраства,

б) – совпадение экспериментально наблюдаемых дистанций между атомами при их помещении в центры полиэдров,

в) – предложенный метод полиэдрального моделирования обладает описательными и предсказательными свойствами.

Литература

1. V.A. Blatov, A.P. Shevchenko, V.N. Serezhkin, Crystal space analysis by means of Voronoy-Dirichlet polyhedra, Acta Cryst. 1995, A51, 909–916.

2. А.В. Шевельков, Супрамолекулярные клатраты: от экзотических веществ к материалам нового поколения, Соросовский образовательный журнал, т.8, №2, 2004.

3. Е.А. Андреев, Некоторые геометрические закономерности формирования наноструктур и их предсказательные возможности, тезисы II Международной научной конференции “Наноструктурные материалы – 2010”, Киев, Украина. С. 34. (2010).

4. Р. Бейдер, Атомы в молекулах. Квантовая теория. – М.: Мир, (2001).

5. Hilgenfeldt, S., AM Kraynik, DA Reinelt, and JM Sullivan, The Structure of Foam Cells: Isotropic Plateau Polyhedra, Europhysics Letters, 67:3, 484–490, (2004).

6. J. Lopez Cacheiro, B. Fernandez, D. Marchesan, S. Coriani and A. Rizzo, Coupled cluster calculations of the ground state potential and interaction properties of the mixed dimers of helium, neon and argon, Mol. Phys. 102(1), 101–110 (2004).

7. T. P. Haley and S. M. Cybulski, Ground state potential energy curves for He-Kr, Ne-Kr, Ar-Kr, and Kr2: Coupled-cluster calculations and comparison with experiment, J. Chem. Phys. 119(11), 54875496 (2003).

8. Cambridge Structural Database System. Version 5.27. Cambridge Crystallo-graphic Data: Centre, 2006.

8. K. T. Tang and J. P. Toennies, The van der Waals potentials between all rare gas atoms from He to Rn, J. Chem. Phys. 118, 497 (2003).

9. T. Ozaki, H. Kino, Numerical atomic basis orbitals from H to Kr, Phys. Rev. B 69, 195113 (2004).

10. В.Н. Сережкин, Д.В. Пушкин, Кристаллохимические радиусы и координационные числа атомов, Учебное пособие, (2004).

11. С. С. Бацанов, Структурная химия. Факты и зависимости, М. 2000, 291 с.